Les proportions divines
Elles se retrouvent fréquemment dans la nature, en particulier dans les structures des organismes vivants.
Les proportions d'or , par exemple, sont couramment observées dans les proportions des différentes parties d'un corps humain, comme dans les proportions entre les doigts, les membres et la tête.
Les proportions de Fibonacci sont également couramment observées dans les phénomènes naturels tels que les spirales dans les coquillages, les feuilles et les branches des arbres, les fleurs, les fruits et les graines, ainsi que les vagues de l'océan et les tourbillons de gaz dans les galaxies.
Les mathématiques de ces proportions sont liées à des phénomènes comme la croissance exponentielle et la régularité dans les systèmes naturels.
Les proportions divines sont des rapports numériques utilisés dans l'architecture, l'art et la musique pour créer des formes et des sons harmonieux. Les plus célèbres sont le nombre d'or (1,618) et le rapport de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, etc.). Ces rapports sont souvent considérés comme ayant un sens esthétique particulier, et ont été utilisés dans de nombreuses œuvres d'art et de design à travers l'histoire.
HISTOIRE DU NOMBRE D’OR (PHI) Qui a découvert le nombre d'Or ? Le 1er écrit qui mentionne Phi, le nombre d’Or est un traité de mathématiques et de géométrie intitulé “Les Éléments“, dont l'auteur est Euclide , un mathématicien grec, qui vécut aux alentours de -300 avant JC. Le nombre d’Or apparaît dans les œuvres d’art, dans des constructions millénaires, mais aussi partout dans la nature.
Néanmoins, il semblerait que le Nombre d’Or était connu depuis l’antiquité car il apparaît dans des constructions datant de milliers d’années, notamment en Égypte, dans la grande pyramide de Gizeh, attribuée au Pharaon Khéops et datée officiellement à -2500 av JC. Phi se retrouve à quasiment tous les niveaux dimensionnels de cette pyramide. Par exemple en divisant la somme des surfaces des faces visibles par la surface de la base, le résultat est Phi .
Cependant, comme pour beaucoup de questions relevant de l’antiquité, aucun écrit ne peut confirmer la connaissance ou l’utilisation volontaire de ce nombre.
L'appellation “Nombre d’Or” est moderne (moins de 100 ans), et, par le passé, il fut nommé de différentes façons à travers les époques et selon les personnes qui l'ont étudié ou utilisé.
QU'EST CE QUE LE NOMBRE D’OR ET QUEL EST-IL ? Le nombre d'Or est une proportion géométrique issue de la division de deux longueurs. C'est la raison pour laquelle Euclide le nommait "Proportion d’extrême et moyenne raison", et Luca Pacioli ainsi que d'autres savants l’appelaient "Proportion Divine".
Ce nombre est irrationnel, donc son écriture décimale est infinie : 1,618 033 988 749...
Mathématiquement, voici φ (Phi)
φ∼1,6180339887…
(Valeur approchée aux dix premières décimales)
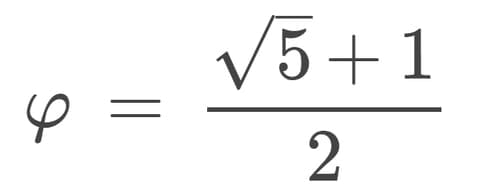
OÚ TROUVER LE NOMBRE D'OR ? Le Nombre d'Or est une constante universelle qui apparaît absolument partout : dans la nature, les plantes, les feuilles, les arbres, les constructions antiques, l'architecture moderne, les œuvres des plus grands artistes, peintres, sculpteurs... En mathématique, en arithmétique et en géométrie sacrée , le nombre d’or induit de nombreux dérivés comme le rectangle d’or, l’angle d’or, spirale d’or, le pentagone régulier ou encore la célèbre suite de Fibonacci .
VIDEO
Beaucoup d'artistes sont fascinés par le nombre d'Or car son utilisation permet des proportions divines , naturelles, équilibrées, harmonieuses et intuitivement parfaites et idéales pour l’œil humain.
La découverte de ce nombre matérialise une concordance concrète et récurrente qui revient sans cesse dans les plus belles œuvres d’art, celles de la nature.
LES PROPRIÉTÉS DU NOMBRE D’OR Le nombre d'or est donc approximativement de 1,6180339887 phi, Φ . Il est souvent nommé la "divine proportion ", car il apparaît très fréquemment dans la nature. Par exemple, le nombre de pétales dans une fleur est très souvent un nombre issu de la suite de Fibonacci .
Ses proportions et les rapports mathématiques qui en découlent sont tellement uniques et équilibrés, que beaucoup de savants y voient un côté divin.
Le nombre possède des propriétés fascinantes dans de nombreux domaines d'applications tels que les mathématiques, la géométrie (rectangle d’or, triangle d’or, angle d’or, spirale d’or, le pentagone…), l’arithmétique mais aussi en phyllotaxie (étude de la disposition des feuilles sur les tiges des plantes).
Lire notre article sur la géométrie sacrée
QUEL EST LE RAPPORT ENTRE LE NOMBRE D’OR ET LA SUITE DE FIBONACCI ? La suite de fibonacci et le nombre d'or
Il existe une relation particulière entre le nombre d'or (1,618...) et la suite de Fibonacci (0, 1, 1, 2, 3, 5, 8, 13, 21 etc...) dans laquelle chaque nombre est la somme des deux nombres qui le précèdent.
Lorsque nous prenons deux nombres qui se suivent dans la suite de Fibonacci, et que l’on divise le plus grand par le plus petit, le résultat est très proche du nombre d'or. Plus les nombres de la suite de Fibonacci sont élevés, plus le résultat se rapproche du nombre d’Or.
Autrement dit, le nombre d'Or apparaît en divisant tout nombre de la suite de Fibonacci par son prédécesseur. Plus les nombres sont grands, plus l'approximation est précise.
Prenons par exemple deux nombres élevés se succédant dans la suite de Fibonacci et divisons le plus grand par le plus petit :
10946 divisé par 6765 = 1,6180339 985218033…
Qu’est ce que la suite de Fibonacci ?
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233...
-----------------------------------
Comment se construit la suite de Fibonacci ? Les deux premiers nombres sont 0 et 1, et ensuite, chaque nombre successif est la somme des deux nombres qui le précède : 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, etc…
-------
Qu'est ce que la Spirale d’or ? La spirale d’or un dérivé direct du nombre d'Or , une forme géométrique issue directement des proportions divines . Elle est constituée de quarts de cercle inscrits dans chaque carré.
C’est une spirale que l'on appelle : « eadem mutata resurgo» = « déplacée, je réapparais à l’identique »
-------
Qu'est ce que l'Angle d’Or ? L’angle d’or est de 137,5° degré.
L'angle d'Or apparaît quand on divise un cercle en deux sections dont les deux longueurs sont dans un rapport égal au nombre d’or. L’angle d’or apparaît de façon très fréquente dans la nature, par exemple, dans la pomme de pin ou le encore le choux romanesco.
Proportion d’extrême et moyenne raison Euclide https://fr.wikipedia.org/wiki/Euclide Le Nombre Scandaleux Platon https://fr.wikipedia.org/wiki/Platon
La Section Dorée Léonard de Vinci https://fr.wikipedia.org/wiki/Leonardo_da_Vinci
La Proportion d’Euclide Fibonacci https://fr.wikipedia.org/wiki/Fibonacci
La Divine Proportion Luca Paciolihttps://fr.wikipedia.org/wiki/Luca_Pacioli
La Section D’Or Adolf Zeisinghttps://fr.wikipedia.org/wiki/Adolf_Zeising
Le Nombre d’Or Matila Ghykahttps://fr.wikipedia.org/wiki/Matila_Ghyka
OU PEUT ON TROUVER LE NOMBRE D'OR DANS L'ART ET L'ARCHITECTURE ?
VIDEO
OÚ TROUVER LE NOMBRE D’OR DANS L’ART, LES TABLEAUX ? Ci-dessous quelques exemples de tableaux incluant le nombre d'OrMona-Lisa de Léonard de Vinci
Ce tableau renferme de multiples rectangles d'or . On peut tracer un rectangle dont la base va du poignet droit à son coude gauche et étendre le rectangle verticalement jusqu'à ce qu'il atteigne le sommet de sa tête. Nous aurons alors un rectangle d'Or.
Ensuite si nous traçons des carrés à l'intérieur de ce rectangle d'or, nous remarquerons que les extrémités de ces nouveaux carrés rejoignent tous les points essentiels de la femme : son œil, son nez, son menton, et le coin de sa bouche.
Léonard de Vinci était aussi un mathématicien, et on dirait qu'il a réalisé ce tableau en utilisant sciemment le rectangle d'or afin de transposer l'harmonie de la géométrie sacrée dans ses œuvres d'art.
L'homme de Vitruve "(L'homme en action)" de Léonard de Vinci
Nous pourrions dessiner de multiples lignes de rectangles sur l' l'Homme de Vitruve et le nombre d'or.
Apparaissent alors trois groupes bien distincts de rectangles d'or : trois groupes, un pour la tête, un pour le torse et un pour les jambes.
"Un vieil homme" par Léonard de Vinci
Léonard de Vinci a étudié le corps humain en se penchant sur les proportions des longueurs des différentes sections du corps. Il a qualifié ce rapport de "proportion divine " et l'a fait apparaître dans plusieurs de ses tableaux. Il l'appelait "La Section Dorée ".
Le croquis de Léonard de Vinci illustrant "Un vieil homme" peut être superposé à un carré décomposé en rectangles, dont plusieurs se rapprochent des rectangles d'or .
“ La naissance de Vénus” De Sandro Boticelli
La naissance de Vénus est une toile réalisée par Sandro Botticelli (1482 environ). On y regarde la déesse Temps recouvrant la planète Vénus d'un manteau. Sur la gauche il y a les dieux du vent (dont Zéphyr), qui ont amené la déesse vers le rivage.
Les dimensions de cette toile (172,5 × 278,5 cm) forment un rectangle d'or et suivent précisément la proportion d'or .
"La Sainte Famille" par Michel-Ange
Nous pouvons remarquer que ce tableau est disposé de façon à ce que les figures majeures soient en alignement avec un Pentagramme ou une étoile d'or .
"Autoportrait" de Rembrandt
Si nous dessinons trois lignes droites dans cette figure. Ensuite, l'image du trait est comprise dans un triangle d'Or . De plus, si une ligne perpendiculaire est tracée en partant du sommet du triangle à sa base, le triangle coupe la base en sections d'Or .
"Les Baigneuses" de Seurat
Seurat a appliqué le nombre d'or sur la majorité de ses tableaux. "Les Baigneuses" est une toile souvent mentionnée pour sa maîtrise des sections dorées subdivisées .
"Le sacrement de la Cène" de Salvador Dali (1904-1989)
Ce tableau est exécuté à l'intérieur d'un rectangle d'or . Ensuite nous pouvons observer un gigantesque dodécaèdre (au-dessus de la table). Puisque ce polyèdre est formé de 12 pentagones réguliers, il est donc directement associé au nombre d'or.
"Planche du nombre d'or" de Fletcher Cox
Le titre de cette réalisation contient carrément le nombre d'Or et cette peinture est divisée en différentes sections de proportions divines issues du nombre d'Or .
"Crucifixion" de Raphaël
Cette peinture est l'un des meilleurs exemples dans lequel nous retrouvons un pentagramme et un triangle d'or . Dans ce tableau, un triangle d'or permet de localiser un de ses pentagrammes sous-jacents.
"Composition avec du gris et du brun clair" de Piet Mondrian
Mondrian pensait fermement que l'Art et les mathématiques étaient intimement liés. Il a associé des figures géométriques simples et des couleurs primaires (bleu, rouge, jaune).
Sa vision est basée sur le fait qu'il est possible de créer n'importe quelle forme à partir des formes géométriques de base. De la même façon, il est possible de créer n'importe quelle couleur à partir de diverses combinaisons de rouge, de bleu et de jaune. Le rectangle d'Or revient quasiment tout le temps dans ses œuvres, aussi on peut raisonnablement dire que c'est l'une des bases de la technique artistique de Piet Mondrian.
ARCHITECTURE, DANS QUEL MONUMENT ANCIEN OU ANTIQUE PEUT ON TROUVER LE NOMBRE D’OR ? Aux quatre coins du monde, de nombreux monuments ont été érigés à l'aide du nombre d'or et de la section d'or qui sont des piliers majeurs de la géométrie sacrée . Cette équation mathématique qui inspire l'harmonie et le divin est à la base d'incroyables et d'innombrables constructions.
Ci-dessous vous trouverez des exemples de monuments exceptionnels, réalisés grâce aux proportions idéales et divines, découlant du nombre d'Or, Phi.
Le rectangle d'or et la section d'or apparaissent de façon particulièrement évidente dans la méthode de construction du Parthénon, qui fût réalisé aux alentours de -450 avant JC. C'est un monument majestueux qui intègre à la fois les constantes de la géométrie sacrée et de nombreux éléments caractéristiques de l'architecture grecque classique, comme les chapiteaux doriques ou les grandes colonnes.
Statue de David
Réalisé au début des années 1500 par Michel-Ange, au cours de la célèbre période de la renaissance, la statue de David est littéralement une incarnation du nombre d'or . A cette époque, de nombreux artistes, dont Michel-Ange, Raphael, Léonard de Vinci, Boticelli se servaient du nombre d'or dans leurs œuvres Ils le nommaient également "le ratio divin " et "le ratio d'or ".
Cathédrale de Mexico
La cathédrale de Mexico est un monument exceptionnel qui a nécessité plus de 200 années de construction. On y trouve un panaché des styles architecturaux Renaissance, baroque et néoclassique. La cathédrale métropolitaine de Mexico fût jadis un des monuments mondial en danger car la structure s'enfonçait à cause du sol boueux. Après des années de rénovation le problème a été endigué et cette magnifique œuvre est à nouveau préservée de l'effondrement.
Le Parthénon
Créé par Phidias, le temple d'Athéna , le Parthénon aurait été détruit dans un incendie, mais de nombreuses répliques ont été créées au cours des siècles. Phidias a exploité le ratio d'or pour bâtir ce que nombreux experts jugent comme l'une de ses plus grandes réalisations.
La grande pyramide de Gizeh
La grande pyramide de Gizeh est tellement invraisemblable qu'elle fait partie des sept merveilles du monde antique . L'érosion de l'extérieur rend les mesures difficiles et discutables, néanmoins les dimensions de "la chambre du roi" font apparaitre bien distinctement Pi et Phi . Attribuée au Pharaon Khéops, cette pyramide unique en son genre aurait été construite aux alentours de -2500 avant JC. C'est la la seule des 7 merveilles du monde qui demeure globalement intacte malgré les milliers d'années d'existence. Elle a résisté à des millénaires d'érosion, et aux nombreux tremblements de terre qui ont secoué Le Caire, et, cela met en évidence le savoir-faire extraordinaire des bâtisseurs égyptiens antiques en terme d'architecture. De nos jours, nous utilisons encore de nombreux théorèmes provenant des mathématiciens Grecques tels que Thalès ou Pythagore, et, il est important de rappeler que ces derniers ont tous été étudié en Egypte pendant des années.
Cathédrale de Chartres
Tout comme beaucoup d'autres cathédrales bâties pendant la période de l'Antiquité, la cathédrale "Notre-Dame de Chartres ", située en France, est un des meilleurs exemples de structures réalisées à partir du nombre d'or et de ses dérivés . La portion ouest de l'ancienne cathédrale romane qui a été conservée témoigne nettement de la méthode de construction, axée sur des proportions harmonieuses directement reliées au nombre d'or.
Le siège des Nations unies
Le Corbusier, Charles-Édouard Jeanneret-Gris de son vrai nom, était un architecte exceptionnel, qui a marqué l'histoire grâce à de nombreuses réalisations très originales. Il a notamment réalisé le bâtiment du siège des Nations unies à New York en se basant sur la section d'or et les proportions du rectangle d'or .
Stupa de Borobudur
le temple bouddhiste Mahayana est un magnifique exemple de monument intégrant la géométrie sacrée, les proportions divines et le nombre d'Or . Une immense statue de Bouddha est positionnée de façon protectrice, surplombant le plus grand temple bouddhiste de la planète.
Porche des cariatides
Ce monument inhérent à l'Acropole grecque, a été érigé selon les proportions divines du nombre d'or, et, il a été pensé à partir de trois rectangles d'or . Le porche est intégré au temple grec nommé "l'Erechtheum", une réalisation dédiée aux dieux, Athéna et Poséidon .
Cathédrale Notre Dame de Paris
Cette cathédrale est un parfait exemple de construction asymétrique dans laquelle on distingue directement l'utilisation de plusieurs rectangles d'or .
OÚ EST CE QUE L'ON PEUT TROUVER LE NOMBRE D'OR DANS LA BIBLE ? Est ce que l’on trouve le nombre d’Or dans la Bible ? La réponse est OUI.
Où figure le nombre d’Or, ou des allusions à ce dernier, dans la Bible ? Nous vous proposons de regarder l’excellente vidéo réalisée par la chaîne youtube : Mysteria dont nous saluons le travail réalisé sur le thème de la géométrie sacrée, les Divines Proportions et la Section Dorée.
VIDEO
-------
BIBLIOGRAPHIE
Bibliographie autour du Nombre d'Orhttps://www.youtube.com/c/mysteria_video
Depuis toujours, les proportions divines ont fasciné les artistes, les architectes et les mathématiciens. Ces rapports numériques, tels que le nombre d'or et le rapport de Fibonacci, sont considérés comme ayant une esthétique particulièrement harmonieuse et sont utilisés pour créer des formes et des sons gracieux.
Les proportions divines sont également fréquemment observées dans la nature, où elles jouent un rôle important dans la croissance et le développement des organismes vivants.
En explorant les proportions divines, nous pouvons découvrir des liens entre les mathématiques, l'art, l'architecture et la nature, ainsi que les principes qui régissent l'harmonie et l'équilibre dans l'univers.
Pyramide Orgone TRISKEL Shungite Cristal de Roche
