La Proporción Áurea, Phi y las proporciones divinas
- Célia Jeandel

- proporciones divinas
- HISTORIA DE LA PROPORCIÓN ÁUREA (PHI)
- ¿Quién descubrió la proporción áurea?
- ¿QUÉ ES LA PROPORCIÓN ÁUREA Y QUÉ ES?
- ¿DÓNDE ENCONTRAR EL NÚMERO DE ORO?
- LAS PROPIEDADES DE LA PROPORCIÓN ÁUREA
- ¿CUÁL ES LA RELACIÓN ENTRE LA PROPORCIÓN ÁUREA Y LA SECUENCIA DE FIBONACCI?
- La secuencia de Fibonacci y la proporción áurea
- ¿Qué es la Espiral Dorada?
- ¿Qué es el ángulo dorado?
- ¿DÓNDE PODEMOS ENCONTRAR LA PROPORCIÓN ÁUREA EN EL ARTE Y LA ARQUITECTURA?
- ¿DÓNDE ENCONTRAR LA PROPORCIÓN ÁUREA EN EL ARTE, LAS PINTURAS? A continuación se muestran algunos ejemplos de tablas que incluyen la proporción áurea.
- ARQUITECTURA, ¿EN QUÉ MONUMENTO ANTIGUO O ANTIGUO PODEMOS ENCONTRAR EL NÚMERO DE ORO?
- ¿DÓNDE PUEDES ENCONTRAR LA PROPORCIÓN ÁUREA EN LA BIBLIA?
proporciones divinas
Se encuentran frecuentemente en la naturaleza, particularmente en las estructuras de los organismos vivos.
Las proporciones áureas , por ejemplo, se observan comúnmente en las proporciones de diferentes partes del cuerpo humano, como en las proporciones entre los dedos, las extremidades y la cabeza.
Las proporciones de Fibonacci también se ven comúnmente en fenómenos naturales como espirales en conchas marinas, hojas y ramas de árboles, flores, frutas y semillas, así como en las olas del océano y remolinos de gas en las galaxias.
Las matemáticas de estas proporciones se relacionan con fenómenos como el crecimiento exponencial y la regularidad en los sistemas naturales.
Las proporciones divinas son proporciones numéricas utilizadas en arquitectura, arte y música para crear formas y sonidos armoniosos. Las más famosas son la proporción áurea (1.618) y la proporción de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, etc.). A menudo se considera que estas proporciones tienen un significado estético particular y se han utilizado en muchas obras de arte y diseño a lo largo de la historia.
HISTORIA DE LA PROPORCIÓN ÁUREA (PHI)
¿Quién descubrió la proporción áurea?
El primer escrito que menciona Phi, la proporción áurea, es un tratado de matemáticas y geometría titulado “Los Elementos”, cuyo autor es Euclides , matemático griego, que vivió hacia el -300 a.C. La proporción áurea aparece en obras de arte, en construcciones milenarias, pero también en toda la naturaleza.
Sin embargo, parece que la Proporción Áurea era conocida desde la antigüedad porque aparece en construcciones que datan de miles de años atrás, en particular en Egipto, en la gran pirámide de Giza, atribuida al faraón Keops y fechada oficialmente en -2500 antes de JC. Phi se encuentra en casi todos los niveles dimensionales de esta pirámide. Por ejemplo, al dividir la suma de las áreas de las caras visibles por el área de la base, el resultado es Phi .
Sin embargo, como ocurre con muchas cuestiones relacionadas con la antigüedad, ningún escrito puede confirmar el conocimiento o el uso voluntario de este número.
El nombre “Proporción Áurea” es moderno (tiene menos de 100 años) y, en el pasado, fue nombrado de diferentes maneras a lo largo de los tiempos y según las personas que lo estudiaron o utilizaron.
¿QUÉ ES LA PROPORCIÓN ÁUREA Y QUÉ ES?
La proporción áurea es una proporción geométrica resultante de la división de dos longitudes. Por eso Euclides la llamó "Proporción de la razón extrema y media", y Luca Pacioli y otros estudiosos la llamaron "Proporción divina".
Este número es irracional, por lo que su escritura decimal es infinita: 1.618 033 988 749...
Matemáticamente, aquí está φ (Phi)
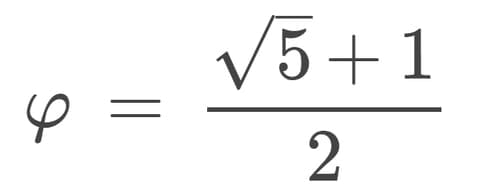
¿DÓNDE ENCONTRAR EL NÚMERO DE ORO?
La Proporción Áurea es una constante universal que aparece absolutamente en todas partes: en la naturaleza, en las plantas, en las hojas, en los árboles, en las construcciones antiguas, en la arquitectura moderna, en las obras de los más grandes artistas, pintores, escultores... matemáticos, en la aritmética y en la geometría sagrada , la La proporción áurea induce numerosas derivadas como el rectángulo áureo, el ángulo áureo, la espiral áurea, el pentágono regular o incluso la famosa secuencia de Fibonacci .
Muchos artistas quedan fascinados por la proporción áurea porque su uso permite proporciones divinas, naturales, equilibradas, armoniosas e intuitivamente perfectas e ideales para el ojo humano.
El descubrimiento de este número materializa una concordancia concreta y recurrente que regresa constantemente en las obras de arte más bellas, las de la naturaleza.
LAS PROPIEDADES DE LA PROPORCIÓN ÁUREA
Por tanto, la proporción áurea es aproximadamente 1,6180339887 . Está representado por la letra griega phi, Φ . A menudo se la llama " proporción divina ", porque aparece con mucha frecuencia en la naturaleza. Por ejemplo, el número de pétalos de una flor suele ser un número de la secuencia de Fibonacci .

Sus proporciones y las relaciones matemáticas que resultan de ellas son tan únicas y equilibradas que muchos estudiosos ven en ellas un lado divino.
El número tiene propiedades fascinantes en muchos campos de aplicación como las matemáticas, la geometría (rectángulo áureo, triángulo áureo, ángulo áureo, espiral áurea, pentágono, etc.), la aritmética pero también en la filotaxis (estudio de la disposición de las hojas en los tallos de las plantas). ).
Lea nuestro artículo sobre geometría sagrada
¿CUÁL ES LA RELACIÓN ENTRE LA PROPORCIÓN ÁUREA Y LA SECUENCIA DE FIBONACCI?
La secuencia de Fibonacci y la proporción áurea
Existe una relación especial entre el número áureo (1.618...) y la secuencia de Fibonacci (0, 1, 1, 2, 3, 5, 8, 13, 21 etc...) en la que cada número es la suma de los dos números que lo preceden.
Cuando tomamos dos números que se suceden en la secuencia de Fibonacci y dividimos el mayor por el menor, el resultado es muy cercano a la proporción áurea. Cuanto más altos sean los números en la secuencia de Fibonacci, más se acercará el resultado a la proporción áurea.
En otras palabras, la proporción áurea aparece dividiendo cualquier número de la secuencia de Fibonacci por su predecesor. Cuanto mayores sean los números, más precisa será la aproximación.
Por ejemplo, tomemos dos números grandes uno detrás del otro en la secuencia de Fibonacci y dividamos el mayor por el menor:
10946 dividido por 6765 = 1,6180339 985218033…
-----------------------------------
-----------------------------------
¿Cómo se construye la secuencia de Fibonacci?
Los primeros dos números son 0 y 1, y luego cada número sucesivo es la suma de los dos números que lo preceden: 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3 + 5=8,etc.
-------
¿Qué es la Espiral Dorada?
La espiral dorada es un derivado directo de la proporción áurea , una forma geométrica derivada directamente de proporciones divinas . Se compone de cuartos de círculo inscritos en cada cuadrado.

Es una espiral que llamamos:
“ eadem mutata resurgo ”
=
“Desplazado, reaparezco idénticamente”

-------
¿Qué es el ángulo dorado?
El ángulo áureo es de 137,5° grados.
El ángulo áureo aparece cuando dividimos un círculo en dos secciones cuyas dos longitudes están en una proporción igual a la proporción áurea. El ángulo dorado aparece con mucha frecuencia en la naturaleza, por ejemplo, en la piña o en la col romanesco.

Proporción de razón extrema y media
Euclides
https://fr.wikipedia.org/wiki/Euclide
El número escandaloso
Platón
https://fr.wikipedia.org/wiki/Platón
La sección dorada
Leonardo DeVinci
https://fr.wikipedia.org/wiki/Leonardo_da_Vinci
La proporción de Euclides
Fibonacci
https://fr.wikipedia.org/wiki/Fibonacci
La proporción divina
luca pacioli
https://fr.wikipedia.org/wiki/Luca_Pacioli
La sección dorada
Adolfo Zeising
https://fr.wikipedia.org/wiki/Adolf_Zeising
La proporción áurea
Matila Ghyka
https://fr.wikipedia.org/wiki/Matila_Ghyka
¿DÓNDE PODEMOS ENCONTRAR LA PROPORCIÓN ÁUREA EN EL ARTE Y LA ARQUITECTURA?
¿DÓNDE ENCONTRAR LA PROPORCIÓN ÁUREA EN EL ARTE, LAS PINTURAS?
A continuación se muestran algunos ejemplos de tablas que incluyen la proporción áurea.
Mona Lisa de Leonardo da Vinci
Esta pintura contiene múltiples rectángulos dorados . Puedes dibujar un rectángulo con la base desde tu muñeca derecha hasta tu codo izquierdo y extender el rectángulo verticalmente hasta llegar a la parte superior de tu cabeza. Entonces tendremos un rectángulo dorado.
Luego, si dibujamos cuadrados dentro de este rectángulo dorado, notaremos que los extremos de estos nuevos cuadrados unen todos los puntos esenciales de la mujer: su ojo, su nariz, su barbilla y la comisura de su boca.
Leonardo da Vinci también era matemático y parece que creó esta pintura conscientemente utilizando el rectángulo áureo para transponer la armonía de la geometría sagrada a sus obras de arte.
Hombre de Vitruvio "(Hombre en acción)" de Leonardo da Vinci
Podríamos dibujar múltiples líneas de rectángulos sobre el Hombre de Vitruvio y la proporción áurea.
Aparecen entonces tres grupos muy distintos de rectángulos dorados : tres grupos, uno para la cabeza, otro para el torso y otro para las piernas.
“Un anciano” de Leonardo da Vinci
Leonardo da Vinci estudió el cuerpo humano observando las proporciones de las longitudes de diferentes secciones del cuerpo. Llamó a esta relación " proporción divina " y la hizo aparecer en varios de sus cuadros. La llamó “ La Sección Áurea ”.
El boceto de Leonardo da Vinci que ilustra "Un anciano" se puede superponer a un cuadrado dividido en rectángulos, varios de los cuales se asemejan a rectángulos dorados .
“El nacimiento de Venus” de Sandro Boticelli
El nacimiento de Venus es una pintura de Sandro Botticelli (hacia 1482). Vemos a la diosa Tiempo cubriendo el planeta Venus con un manto. A la izquierda están los dioses del viento (incluido Céfiro), que llevaron a la diosa a la orilla.
Las dimensiones de este lienzo (172,5 × 278,5 cm) forman un rectángulo dorado y siguen exactamente la proporción áurea .
"La Sagrada Familia" de Miguel Ángel
Podemos notar que esta tabla está dispuesta de manera que las figuras principales estén alineadas con un Pentagrama o una estrella dorada .
“Autorretrato” de Rembrandt
Si dibujamos tres líneas rectas en esta figura. Luego, la imagen de la línea se incluye en un triángulo áureo . Además, si se traza una línea perpendicular desde el vértice del triángulo hasta su base, el triángulo corta la base en secciones de oro .
“Los bañistas” de Seurat
Seurat aplicó la proporción áurea a la mayoría de sus pinturas. "Les Baigneuses" es una pintura a menudo mencionada por su dominio de las secciones áureas subdivididas .
“El Sacramento de la Última Cena” de Salvador Dalí (1904-1989)
Esta pintura está ejecutada dentro de un rectángulo dorado . Luego podemos observar un gigantesco dodecaedro (encima de la mesa). Dado que este poliedro se compone de 12 pentágonos regulares, está directamente asociado con la proporción áurea.
“Gráfico de proporción áurea” de Fletcher Cox
El título de esta creación contiene directamente la proporción áurea y esta pintura está dividida en diferentes secciones de proporciones divinas derivadas de la proporción áurea.
“Crucifixión” de Rafael
Este cuadro es uno de los mejores ejemplos en el que encontramos un pentagrama y un triángulo áureo . En esta pintura, un triángulo dorado permite localizar uno de sus pentagramas subyacentes.
“Composición con gris y marrón claro” de Piet Mondrian
Mondrian creía firmemente que el arte y las matemáticas estaban estrechamente vinculados. Combinó figuras geométricas simples y colores primarios (azul, rojo, amarillo).
Su visión se basa en el hecho de que es posible crear cualquier forma a partir de formas geométricas básicas. Asimismo, es posible crear cualquier color a partir de varias combinaciones de rojo, azul y amarillo. El Rectángulo Áureo aparece casi todo el tiempo en sus obras, por lo que podemos decir razonablemente que es una de las bases de la técnica artística de Piet Mondrian.
ARQUITECTURA, ¿EN QUÉ MONUMENTO ANTIGUO O ANTIGUO PODEMOS ENCONTRAR EL NÚMERO DE ORO?
En todo el mundo, se han erigido muchos monumentos utilizando la proporción áurea y la sección áurea , que son pilares importantes de la geometría sagrada . Esta ecuación matemática que inspira armonía y lo divino es la base de increíbles e innumerables construcciones.
A continuación encontrará ejemplos de monumentos excepcionales, creados gracias a las proporciones ideales y divinas, que surgen del número áureo, Phi.
El Partenón
El rectángulo áureo y la sección áurea aparecen particularmente evidentes en el método de construcción del Partenón, que se construyó alrededor del -450 a.C. Se trata de un majestuoso monumento que integra tanto las constantes de la geometría sagrada como muchos elementos característicos de la arquitectura clásica griega, como los capiteles dóricos o las grandes columnas.
estatua de david
Realizada a principios del siglo XVI por Miguel Ángel, durante el famoso período renacentista, la estatua de David es literalmente una encarnación de la proporción áurea . En aquella época, muchos artistas, entre ellos Miguel Ángel, Rafael, Leonardo da Vinci y Boticelli, utilizaban en sus obras la proporción áurea, también la llamaban " la proporción divina " y " la proporción áurea ".
Catedral de la Ciudad de México
La Catedral de la Ciudad de México es un monumento excepcional que tardó más de 200 años en construirse. Hay una mezcla de estilos arquitectónicos renacentista, barroco y neoclásico. La Catedral Metropolitana de la Ciudad de México fue alguna vez uno de los monumentos del mundo en peligro porque la estructura se estaba hundiendo debido al terreno fangoso. Después de años de renovación el problema fue contenido y esta magnífica obra se preserva una vez más del colapso.
El Partenón
Creado por Fidias, el templo de Atenea , se dice que el Partenón fue destruido en un incendio, pero se han creado muchas réplicas a lo largo de los siglos. Fidias aprovechó la proporción áurea para construir lo que muchos expertos consideran uno de sus mayores logros.
La gran pirámide de giza
La Gran Pirámide de Giza es tan increíble que es una de las Siete Maravillas del Mundo Antiguo . La erosión del exterior hace que las mediciones sean difíciles y cuestionables; sin embargo, las dimensiones de la "cámara del rey" hacen que Pi y Phi aparezcan muy claramente. Atribuida al faraón Keops, esta pirámide única fue construida alrededor del 2500 a.C. Es la única de las 7 maravillas del mundo que permanece generalmente intacta a pesar de miles de años de existencia. Ha resistido milenios de erosión y los numerosos terremotos que sacudieron El Cairo, y esto pone de relieve el extraordinario conocimiento de los antiguos constructores egipcios en términos de arquitectura. Hoy en día todavía utilizamos muchos teoremas de matemáticos griegos como Tales o Pitágoras, y es importante recordar que todos ellos fueron estudiados en Egipto durante años.
Catedral de Chartres
Al igual que muchas otras catedrales construidas durante el período de la Antigüedad, la catedral " Notre-Dame de Chartres ", ubicada en Francia, es uno de los mejores ejemplos de estructuras realizadas a partir de la proporción áurea y sus derivados . La parte occidental de la antigua catedral románica que se conserva muestra claramente el método de construcción, centrado en proporciones armoniosas directamente relacionadas con la proporción áurea.
La sede de las Naciones Unidas
Le Corbusier, cuyo verdadero nombre es Charles-Édouard Jeanneret-Gris, fue un arquitecto excepcional, que dejó su huella en la historia gracias a numerosas realizaciones muy originales. En particular, diseñó el edificio de la sede de las Naciones Unidas en Nueva York basándose en la sección áurea y las proporciones del rectángulo áureo .
Estupa de Borobudur
El templo budista Mahayana es un magnífico ejemplo de monumento que integra la geometría sagrada, las proporciones divinas y la proporción áurea . Una enorme estatua de Buda está colocada de manera protectora, con vistas al templo budista más grande del planeta.
Pórtico de las Cariátides
Este monumento, inherente a la Acrópolis griega, fue erigido según las divinas proporciones de la proporción áurea, y fue diseñado a partir de tres rectángulos áureos . El pórtico está integrado en el templo griego llamado "Erecteum", creación dedicada a los dioses Atenea y Poseidón .
Catedral de Notre Dame de París
Esta catedral es un perfecto ejemplo de construcción asimétrica en la que podemos distinguir directamente el uso de varios rectángulos áureos .
¿DÓNDE PUEDES ENCONTRAR LA PROPORCIÓN ÁUREA EN LA BIBLIA?
¿Se encuentra la proporción áurea en la Biblia? La respuesta es sí.
¿Dónde aparece la Proporción Áurea, o las alusiones a ella, en la Biblia? Los invitamos a ver el excelente video producido por el canal de YouTube: Mysteria, cuyo trabajo saludamos sobre el tema de la geometría sagrada, las Divinas Proporciones y la Sección Áurea.
-------
BIBLIOGRAFÍA
Bibliografía sobre la proporción áurea
Fuente: Canal de YouTube de Mysteria.
https://www.youtube.com/c/mysteria_video
Las proporciones divinas siempre han fascinado a artistas, arquitectos y matemáticos. Se considera que estas proporciones numéricas, como la proporción áurea y la proporción de Fibonacci, tienen una estética particularmente armoniosa y se utilizan para crear formas y sonidos elegantes.
Las proporciones divinas también se observan con frecuencia en la naturaleza, donde desempeñan un papel importante en el crecimiento y desarrollo de los organismos vivos.
Al explorar las proporciones divinas, podemos descubrir conexiones entre las matemáticas, el arte, la arquitectura y la naturaleza, así como los principios que gobiernan la armonía y el equilibrio en el universo.
Te puede interesar
Sur le même sujet...

Mejor venta:
Lo que dicen nuestros clientes:
Artículos recientes
- Electrosensibilidad: comprender y actuar
- Descubre Las Piedras de Piscis: Armonía y Compasión
- Descubre Las Piedras de Acuario: Paz Interior y Espiritualidad
- Descubre las Piedras de Capricornio: Estabilidad y Desarrollo Personal
- Descubre las Piedras de Sagitario: Sabiduría e Introspección
- Descubre las Piedras de Aries: Pasión y Coraje






-
57.00 €
67.00 €Prix régulier 67.00 € Prix réduit 57.00 € - Unit price
- Économisez 10.00 € (-15%)
¡Tu tercer artículo es GRATIS hoy! Elígelo de toda la tienda
Últimas piezas:
¿Te gustan nuestros artículos? Síganos !
Recibe nuestros nuevos artículos del blog de bienestar y aprovecha nuestras ofertas especiales



































c’est la plus belle chose que l’homme a essayé de saisir, parce qu il n est pas défini on a jamais pu definir combien de chiffes après la virgule
Bravo pour l’article! Le nombre d’or est fascinant. Cette vidéo le présente vraiment bien : https://youtu.be/I1QmGqCVq1Q
Merci pour cette découverte ! Coïncidence! Hasard ! Ou bien !!! Toujours est il qu’hier au soir je m’interrogeais sur révélation 13-18 !! Au cours d’une lecture concernant le nouvel ordre mondial, le WEF de Klaus Schwarzenegger et des élites mondialisés sataniques ! Et vous m’apporter une réponse essentielle (moi qui n’aie pas l’intelligence du calcul de ce nombre) à savoir le sionisme ! Et la relation entre le judaisme qui cherche toujours un messie guerrier lui convenant ! et le Christianisme ayant trouvé le messie rédempteur de l’humanité… je comprends mieux la volonté diabolique de Sion de détruire depuis Jesus le Christianisme sur terre, et les événements Covid de cette fausse pandémie en est l’exemple et la fenêtre d’opportunité ! Et ils ne s’en cachent plus, au contraire. « Le livre de la Révélation » est la lecture essentielle aujourd’hui, car elle correspond pile aux évènements qui se passent en cette période de la vie de l’humanité. Famine, tremblement de terre, et surtout l’a chevauchée des 4cavaliers, mais la Victoire Divine finale ……
Waouhhhh.. Puissant! Pas simple pour tout capter….